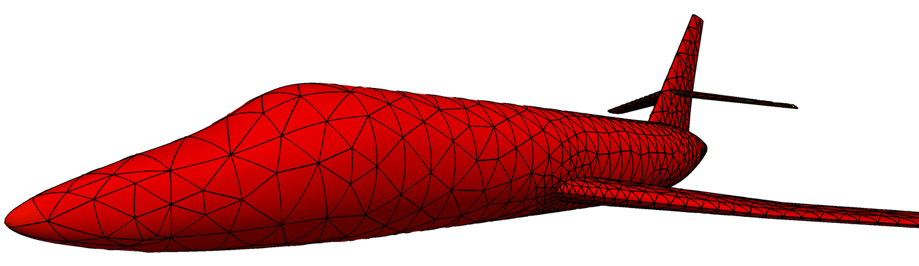
Numerical modelling plays a basic role in applied science and engineering. Its application to problems of industrial interest that requires certified solutions relies on two key ingredients: the development of reliable mesh generation algorithms and the development of solvers that provides bounds on the solution accuracy. Our research focusses on these two issues.

On the one hand, we are developing a framework to generate curved high-order meshes for arbitrary curved geometries. In particular, we target on delivering valid (non-tangled) and high-quality meshes. On the other hand, we are developing adaptive strategies for transient and stationary problems that provide error bounds in the quantity of interest below a user-defined tolerance. In addition, we are also developing methodologies that provide accurate low-cost approximations ideof stochastic finite elements simulations.

A distortion measure to validate and generate curved high-order meshes on CAD surfaces with independence of parameterization
Gargallo-Peiró, A.; Roca, X.; Peraire, J. and Sarrate, J.
International Journal for Numerical Methods in Engineering , Vol. 106, Issue 13, pp. 1100-1130, 2016

A semi-analytical scheme for highly oscillatory integrals over tetrahedra
Hospital-Bravo, R.; Sarrate, J. and Díez, P.
International Journal for Numerical Methods in Engineering , Vol. 111, Issue 8, pp. 703-723, 2017

High-order mesh curving by distortion minimization with boundary nodes free to slide on a 3D CAD representation
Ruiz-Gironés, E.; Roca X.; Sarrate, J.
Computer-Aided Design , Vol. 72, pp. 52-64, 2016

Enhanced goal-oriented error assessment and computational strategies in adaptive reduced basis solver for stochastic problems
Serafin, K.; Magnain, B.; Florentin, E.; Parés, N. and Díez, P.
International Journal for Numerical Methods in Engineering , Vol. 110, Issue 5, pp. 440-466, 2017