Arash Moaven received two Masters, one in Structural Engineering in Ferdowsi University of Mashhad in Iran and the other one in Computational Mechanics of Materials and Structures in Universität Stuttgart in Germany. He is now a PhD candidate in Erasmus Mundus Joint Doctorate SEED at Universitat Politècnica de Catalunya and Université Libre de Bruxelles.

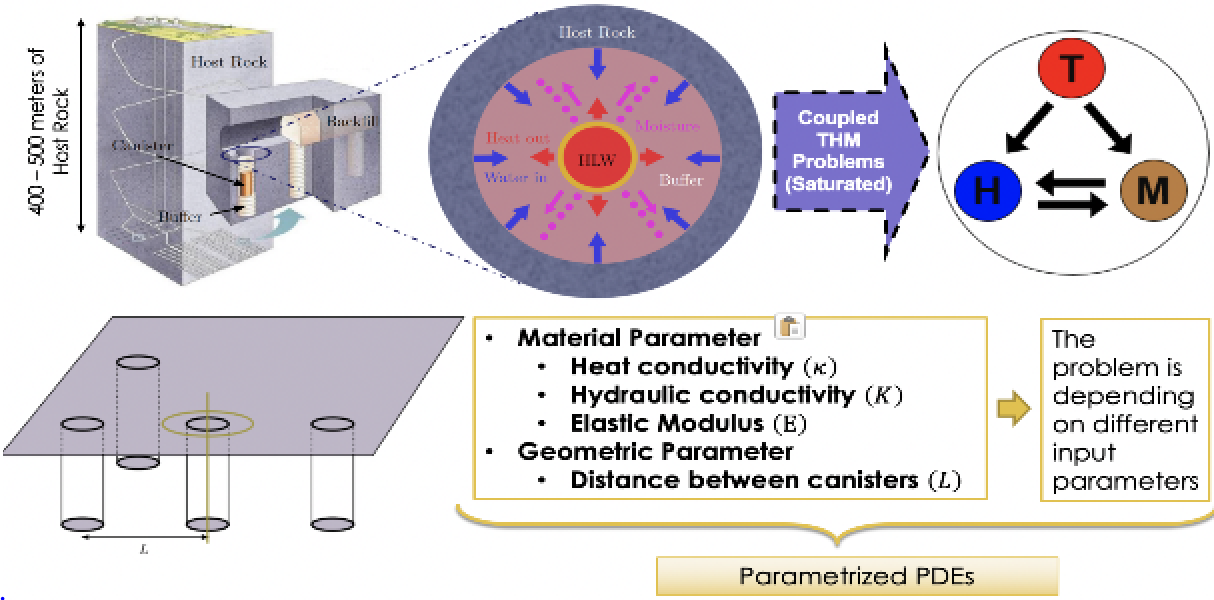
Nuclear power plants for electricity generation produce byproducts including wastes that remain radioactive for thousands of years. The disposal and storage of high-level radioactive wastes are extremely complex problems that currently remain unresolved. One the proposal for long term storage is the use of deep underground repositories where wastes are isolated and avoid interaction with the environment. There is, therefore, a high interest in the study of the long-term behavior of such underground repositories. Several efforts have been made in the construction and monitorization of such repositories and also in its numerical simulation. The problem under consideration is of transient nature and requires the solution of three coupled physics: i) a thermal part including the heat released by the wastes; ii) the mechanical behavior of the canister holding the wastes, the isolation system and the underground host rock; and, iii) the flow of natural water present in any underground porous media. Thermo Hydro-Mechanical (THM) problems are usually solved for parametric studies, parameter identification or repository-related design decisions and, therefore, the availability of explicit parametric solutions could be a large advantage in term of the computational effort required. In this talk we will present generalized parametric solutions of the steady state and transient THM problems obtained via Proper Generalized Decomposition (PGD). We will show how to state the discrete problem in order to use the encapsulated version of PGD for material parameters and for geometrical parameters. We will also explain a novel time integration scheme for parametric parabolic problems.