Universitat Politècnica de Catalunya and Swansea University
29 November 2024
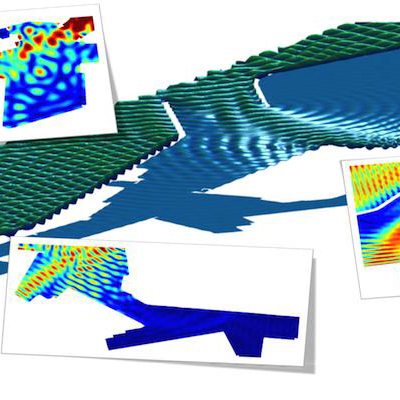
Mathematical and computational modelling relies on methods and tools providing numerical solutions to complex simulation problems. These techniques range from the pre-processing (CAD interface, automatic meshing, data acquisition…) to verification and validation via a posteriori error assessment and adaptivity, showcasing a diversity of state-of-the-art solvers. We aim at designing and implementing efficient methodologies producing high-fidelity solutions with certified accuracy, adapted to each particular problem under analysis. We develop these innovative methodologies both in academic codes (with flexibility to intrusively test new ideas) and professional or commercial codes, certified by our industrial partners, with a large variety of models and methods, extensively tested and computationally optimized. In the latter case we aim at using non-intrusive implementations. The problems under consideration cover a wide range of applications:
In the framework of seeking real-time responses to multiparametric problems, we are particularly concerned with the efficiency of the numerical methodologies and the credibility of the solutions provided. Thus, from a methodological viewpoint, the current ongoing research includes:






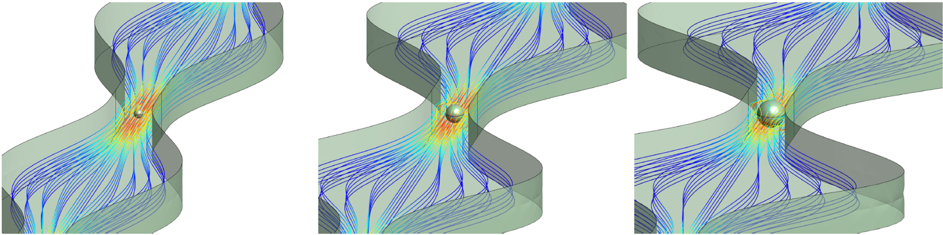
Universitat Politècnica de Catalunya and Swansea University
29 November 2024
Universitat Politècnica de Catalunya
13 November 2024
Thomas B. J. Di Giusto
Universitat Politècnica de Catalunya and Swansea University
24 January 2024
Universitat Politècnica de Catalunya and École des Ponts ParisTech
4 December 2023
Paulo R. Refachinho de Campos
Universitat Politècnica de Catalunya and Swansea University
27 September 2022
Universitat Politècnica de Catalunya
6 April 2022
Universitat Politècnica de Catalunya
10 February 2021
Universitat Politècnica de Catalunya
23 July 2021
Universitat Politècnica de Catalunya
5 July 2021
Ecole Centrale de Nantes and Universitat Politècnica de Catalunya
15 February 2021